3. Parallele Multiplikation
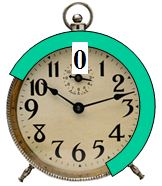
Modulo-Rechnung kennen wir vom Ablesen einer Uhr.
Uhren mit Digitalanzeige konnten sich nie flächendeckend durchsetzen. Das liegt wohl neben der Ästhetik vor allem an zwei Nachteilen der Digitaluhren. Erstens sagen sie zwar, wie spät es genau ist, meist wollen wir es aber nur ungefähr wissen und haben einen kleinen Transfer zu leisten (z.B. von 10:54:49 nach „fünf vor Elf“). Zweitens – und das ist wohl wichtiger – wollen wir meistens gar nicht wissen, wie spät es gerade ist, sondern wie lange es noch bis zu einem bestimmten Termin dauert. Und genau das lässt sich bei der Analoguhr mit einem Blick ablesen: Wenn Sie um 17:00 verabredet sind, wie lange haben Sie noch Zeit? Auf der Uhr im Bild wären es noch knapp 7 Stunden (grüner Bogen).
Wenn wir die 12 durch 0 ersetzen, ist das Zifferblatt ein praktisches Hilfsmittel für die Addition modulo 12. Der grüne Bogen steht dann für (10 + 7) mod 12 = 5.
Natürlich kann man die Arithmetik modulo 12 auch auf die
Multiplikation und weitere Rechenoperationen ausdehnen, auch wenn die Uhr
dabei dann nicht mehr hilft.
Der chinesische Restsatz
sagt in einer speziellen Form: Wenn zwei Zahlen m_1
und m_2 teilerfremd sind und für
eine Zahl x bekannt ist, dass
x mod m_1 = a_1 und
x mod m_2 = a_2,
dann gibt es genau eine Lösung x im Bereich von 0
bis m_1 · m_2 - 1.
Mit m_1 = 99 und m_2 = 101
können wir also jede Zahl von 0 bis 99·101 - 1 = 9998 bestimmen, wenn wir
ihre beiden Reste modulo 99 und 101 kennen.
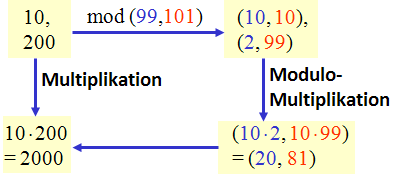
Die nebenstehende Abbildung zeigt im Prinzip, wie man damit die Multiplikation mit Ergebnissen im Bereich 0, ..., 9998 in zwei Teilmultiplikationen von Zahlen in den Bereichen 0, ..., 98 und im Bereich 0, ..., 100 zerlegen kann.
Wählt man statt 99 und 101 z.B. zwei teilerfremde Zahlen knapp unterhalb von 1032, so kann man eine Multiplikation von Zahlen bis knapp 1064 in zwei 32-Bit-Multiplikationen zerlegen, die auf zwei Prozessoren parallel ausgeführt werden können. Der chinesische Restsatz gilt aber nicht nur für zwei, sondern für beliebig viele teilerfremde Modulo-Zahlen. Damit könnte man große Multiplikationen auf viele Prozessorkerne verteilen. Das lohnt sich allerdings erst dann, wenn man mehr als eine Rechenoperation ausführt, bevor man das Ergebnis benötigt. Denn die Rückberechnung des Ergebnisses kostet ja auch Rechenzeit.
Der chinesische Restsatz ist in mathGUIde eingebaut. Hier folgt das Berechnungsbeispiel aus der Abbildung:
Fortsetzung: Karazuba-Multiplikation
