Auch scheinbar einfache Algorithmen lassen sich oft noch optimieren.
auf diesem Streifzug untersuchen wir, ob die aus der Schule bekannte schriftliche Multiplikation noch Verbesserungspotenzial hat.
1. Multiplikation durch Addition
Falls Sie sich noch an das schriftliche Rechnen in der Schule erinnern oder jemals in die Verlegenheit kamen, nur mit Bleistift und Papier eine größere Multiplikation durchzuführen, werden Sie ein Gefühl dafür haben, dass Multiplizieren viel aufwendiger ist als Addieren. Woran liegt das?
Probieren Sie bitte einmal, zwei vierstellige Zahlen schriftlich zu addieren und zu multiplizieren.
Sieht Ihr Zettel etwa so aus:
Wie verhält sich die Rechenzeit zur Größe der Zahlen beim schriftlichen Multiplizieren?
Wir haben jede Ziffer des linken Faktors mit jeder Ziffer des rechten Faktors multipliziert. Im Beispiel haben wir 4·4 = 16 Einzelmultiplikationen durchgeführt.
Für das Produkt zweier n-stelliger Zahlen brauchen wir also n^2 einzelne Multiplikationen. Dazu kommt noch das Aufaddieren am Ende, das aber am gesamten Rechenaufwand bei großen Zahlen kaum eine Rolle spielt. Die Zeit ist demnach proportional zum Produkt der Längen beider Zahlen.
Zum Vergleich: Beim schriftlichen Addieren zweier n-stelliger Zahlen braucht man nur n Additionen von einzelnen Ziffern (und maximal noch einmal so viele Additionen für die Überträge). Die Rechenzeit steigt hier also nur linear mit n an!

Meine erste, vom Taschengeld erworbene Rechenmaschine
Die relative Einfachheit der Addition schlägt sich auch in der Geschichte der mechanischen Rechenmaschinen nieder. Bevor in den 1970er-Jahren der Taschenrechner seinen Siegeszug antrat, waren preiswerte mechanische Additionshilfen weit verbreitet. Maschinen, die auch multiplizieren konnten, waren dagegen sehr teuer und langsam.

Das Geheimnis dieser Addiatoren waren Doppelzahnstangen (links im Bild blau eingezeichnet), in die ein Stift gesteckt wurde, um die Ziffern zu verschieben. Um z.B. im linken Bild 30 zu addieren, steckt man den Stift in das mit 3 markierte Loch der hervorgehobenen Zehnerstange und zieht ihn bis zum unteren Ende. Wenn man aber z.B. 70 addieren möchte, ist das entsprechende Loch rot markiert. Das bedeutet, dass man nicht nach unten schieben darf (sonst käme man ja aus dem erlaubten Ziffernbereich bis 9 heraus, sondern nach oben. Statt 70 zu addieren, subtrahiert man also 30 (=100-70) und korrigiert den Fehler, indem man anschließend 100 addiert. Das geht aber in einem Rutsch durch den oben umgebogenen Weg!
Wegen der Unerschwinglichkeit von Multiplikationsmaschinen hat man sich früher beholfen, indem man die Multiplikation mit Hilfe von Logarithmen auf die Addition zurückgeführt hat.
Die folgende Abbildung zeigt das Prinzip:
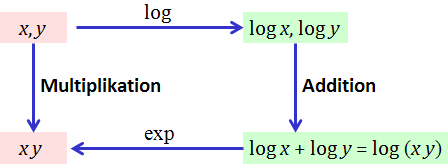
Statt die Multiplikation x·y direkt durchzuführen, berechnet man die Logarithmen von x und y, addiert diese und wendet auf die Summe die Umkehrfunktion (Exponentialfunktion) an, um das Ergebnis zu erhalten.
In der Praxis wurden deshalb Logarithmentafeln zur Basis 10 gedruckt.
Hier sehen Sie einen Auszug aus einer vierstelligen Logarithmentafel:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 300 | 4771 | 4773 | 4774 | 4776 | 4777 | 4778 | 4780 | 4781 | 4783 | 4784 |
| 301 | 4786 | 4787 | 4789 | 4790 | 4791 | 4793 | 4794 | 4796 | 4797 | 4799 |
| 302 | 4800 | 4802 | 4803 | 4804 | 4806 | 4807 | 4809 | 4810 | 4812 | 4813 |
| 303 | 4814 | 4816 | 4817 | 4819 | 4820 | 4822 | 4823 | 4824 | 4826 | 4827 |
| 304 | 4829 | 4830 | 4832 | 4833 | 4834 | 4836 | 4837 | 4839 | 4840 | 4842 |
| 305 | 4843 | 4844 | 4846 | 4847 | 4849 | 4850 | 4852 | 4853 | 4854 | 4856 |
| 306 | 4857 | 4859 | 4860 | 4861 | 4863 | 4864 | 4866 | 4867 | 4869 | 4870 |
| 307 | 4871 | 4873 | 4874 | 4876 | 4877 | 4878 | 4880 | 4881 | 4883 | 4884 |
| 308 | 4886 | 4887 | 4888 | 4890 | 4891 | 4893 | 4894 | 4895 | 4897 | 4898 |
| 309 | 4900 | 4901 | 4902 | 4904 | 4905 | 4907 | 4908 | 4909 | 4911 | 4912 |
Früher war die Berechnung solcher Tafeln mit ungeheuren Mühen verbunden. So verbrachte der Mathematikprofessor Henry Briggs sieben Jahre damit, Logarithmen zur Basis 10 zu berechnen. Heute bräuchte er dazu nur noch auf den roten „Abakus“ zu klicken:
In der Tafel oben steht die Hervorhebung für 3,024 = 100,4806, aber auch für 30,24 = 101,4806 oder 3024 = 103,4806 usw.
Der Auszug zeigt 100 von 10000 Logarithmen der gesamten Tafel, die etwa 20 Buchseiten benötigt.
Im praktischen Gebrauch waren auch siebenstellige Logarithmentafeln, schon ziemlich dicke Wälzer.
Warum hat man denn statt Logarithmentafeln nicht gleich große Multiplikationstafeln gedruckt?
Eine Logarithmentafel ist eindimensional, zu jeder Zahl (in bestimmten Abständen) enthält sie einen Eintrag. Eine Multiplikationstafel dagegen ist zweidimensional: Sie muss zu jedem Paar von Zahlen einen Eintrag enthalten. So würde aus einem handlichen Buch eine riesige Bibliothek!

Sehr naheliegend ist es auch, die Logarithmen direkt auf Linealen aufzutragen und diese grafisch zu addieren. Einen solchen Rechenschieber hatte bis in die siebziger Jahre hinein praktisch jeder Ingenieur. Um z.B. 2·3 zu berechnen kann man die Logarithmen von 2 und 3 addieren, indem man die 2 des unteren Lineals an die 1 (log 1 = 0) des oberen schiebt und nun unter der 3 des oberen Lineals das Ergebnis 6 abliest.
Fortsetzung: Binäre Multiplikation
