2. Zwei Primzahlexperten am Fuße eines Weltwunders
Im Jahr 331 v.Chr. gründete Alexander der Große, der auf seinem Feldzug ein riesiges Weltreich eroberte, die Stadt Alexandria am Nildelta. Nach Alexanders Tod wurde dessen Feldherr Ptolemaios Herrscher von Ägypten. Er ließ den riesigen Leuchtturm bauen, der zu den Sieben Weltwundern zählte, und gründete die später weltberühmte Bibliothek von Alexandria.
Wenige Jahre nach Ptolemaios’ Tod wurde in Kyrene an der heute libyschen Küste der große Universalgelehrte Eratosthenes geboren, der im Auftrag der Könige Ptolemaios II. bis Ptolemaios V. Leiter der Bibliothek von Alexandria war.
Messung des Erdumfangs
Eratosthenes berechnete den Umfang der Erdkugel im Rahmen der damaligen Möglichkeiten recht genau.
Den Umfang der Erdkugel? Galt denn die Erde nicht bis ins späte Mittelalter als Scheibe? Das ist ein immer wieder zu hörender Irrtum. Auch vor Kopernikus, der die Erde aus dem Zentrum rückte, hatte, schon bei den alten Griechen, kein ernstzunehmender Wissenschaftler an der Kugelgestalt der Erde gezweifelt, nicht einmal die Katholische Kirche, der es nur darum ging, dass der Vatikan den Mittelpunkt des Universums markierte. Schon Aristoteles hatte drei Argumente für die Kugelgestalt der Erde angegeben: Das langsame Absinken auslaufender Schiffe am Horizont, den in südlichen Gegenden unterschiedlichen Stand der Sterne und die Tatsache, dass der Erdschatten bei Mondfinsternissen immer kreisrund ist. Seit der Renaissance wurde das Mittelalter gern noch ein bisschen finsterer dargestellt als es wirklich war. Doch mittelalterliche Finsternis gab es in allen Zeitaltern und gibt es heute bis ins Präsidentenamt großer Staaten. Die Legende wurde 1828 weit verbreitet durch die Kolumbus-Biografie des amerikanischen Schriftstellers Washington Irving, in der dieser behauptete, Kolumbus habe beweisen wollen, dass die Erde nicht flach sei.
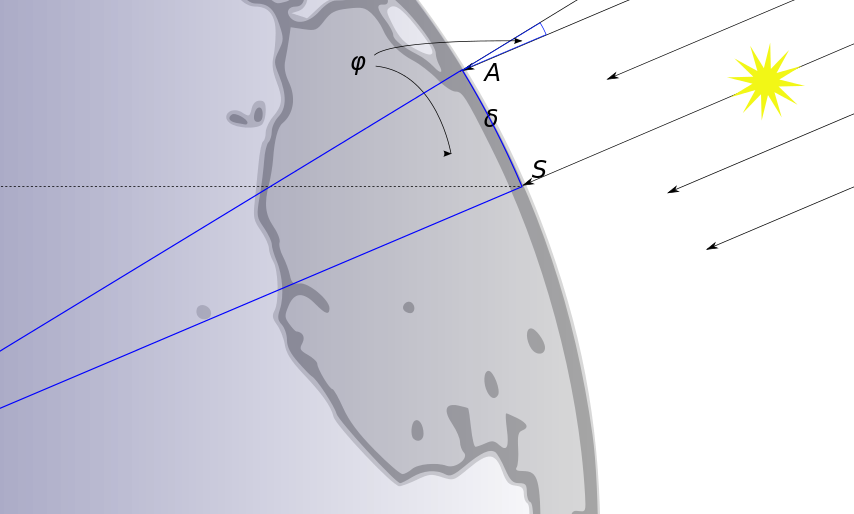
Eratosthenes nutzte folgende durch Messungen gewonnenen Fakten:
- Den Unterschied der mittäglichen Zenitabstände der Sonne in Alexandria und dem südlicheren Syene, heute Assuan (etwa 7°),
- Die Entfernung zwischen Alexandria und Syene,
- die Tatsache, dass diese Entfernung winzig ist im Vergleich zum Abstand zwischen Sonne und Erde, und daher die Sonnenstrahlen auf der Erde so gut wie parallel auftreffen.
So brauchte Eratosthenes nur die Entfernung der beiden Orte mit 360/7 zu multiplizieren und kam damit wahrscheinlich auf einen Fehler von weniger als 10%.
Das Sieb des Eratosthenes
Und was hat das alles mit Primzahlen zu tun?
Danke für die Ermahnung!
Eratosthenes gab eine Methode zum systematischen Auffinden aller Primzahlen bis zu einer vorgegebenen Zahl n an, die er „Sieb“ nannte.
Da 2 die einzige gerade Primzahl ist, schreibt man als weitere Kandidaten nur die ungeraden Zahlen von 3 bis n hin. Im Beispiel n = 100 sieht das so aus:
2 und die ungeraden Zahlen von 3 bis 99:

Alle Vielfachen von 3 können gestrichen werden.
5 ist Primzahl, weil sie durch keine kleinere teilbar ist. Alle Vielfachen von 5 können gestrichen werden.
7 ist Primzahl, weil sie durch keine kleinere teilbar ist (sonst wäre sie schon gestrichen). Alle Vielfachen von 7 können gestrichen werden. 2⋅7, 3⋅7, ... 6⋅7 sind schon als Vielfache kleiner Zahlen gestrichen. Die erste zu streichende Zahl ist also 7⋅7 = 49.
11 ist Primzahl, weil sie durch keine kleinere teilbar ist. Das erste zu streichende Vielfache von 11 wäre 121. Das fällt aber schon aus dem Bereich. Übrig sind also die Primzahlen bis 100.
Der Automat des Eratosthenes
Hier können Sie nochmal den geheimnisvollen zellulären Automaten testen:
Haben Sie es herausgefunden? Wenn man die Schräglinien von der ersten schwarzen aus zählt, sind die weißen Schräglinien auf den Plätzen 2, 3, 5, 7, 11, 13, 17 usw. Die Überschrift „Der Automat des Eratosthenes“ könnte den Griechen allerdings posthum beleidigen. Denn der Automat zeichnet sich eher durch Eleganz als durch Effizienz aus. Die Funktion ist eine Primitivversion des Siebes, das die Vielfachen nicht nur der Primzahlen, sondern aller Zahlen (schwarz) streicht. Im rechten Bereich sieht man senkrechte Trennlinien in gleichmäßig größer werdendem Abstand und Zickzacklinien, die von diesen Wänden teils gespiegelt, teils durchgelassen werden. Die 16 unterschiedlichen Farben werden benötigt um den Zickzacklinien ein „Gedächtnis“ zu verleihen („Ich bin von rechts auf die Trennlinie gestoßen und muss nach links weiter laufen“ etc.).
Die Regeln für diesen Primzahl-Automaten sind entnommen aus: Stephen Wolfram: „A New Kind of Science“, S. 640/Appendix.
Der Automat von Euklid
Zwar sind Euklids Werke überliefert, über sein Leben aber weiß man kaum etwas. Wahrscheinlich hat er um 300 v.Chr. in Alexandria gelebt, zu früh, um Eratosthenes zu begegnen.
Eine seiner Entdeckungen war dieser blaue Automat. Können Sie aus den drei Beispielen auf seine Funktionsweise schließen?
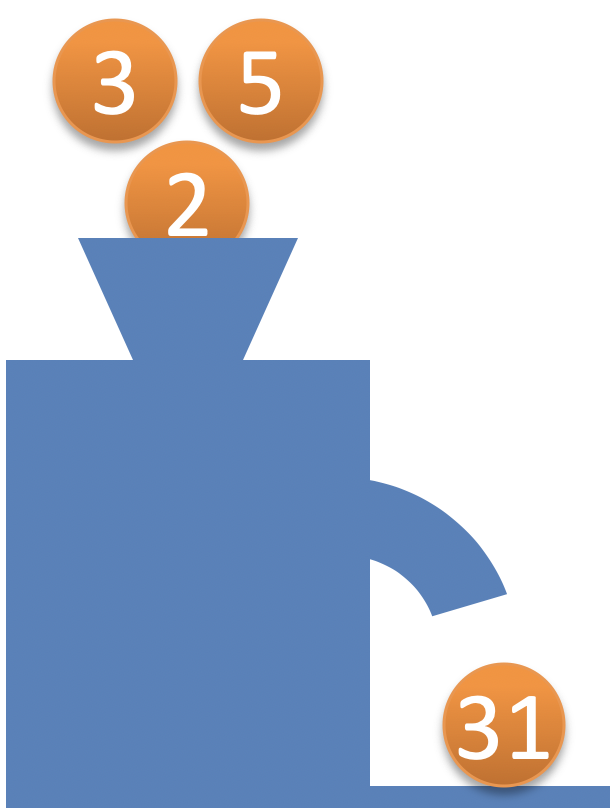
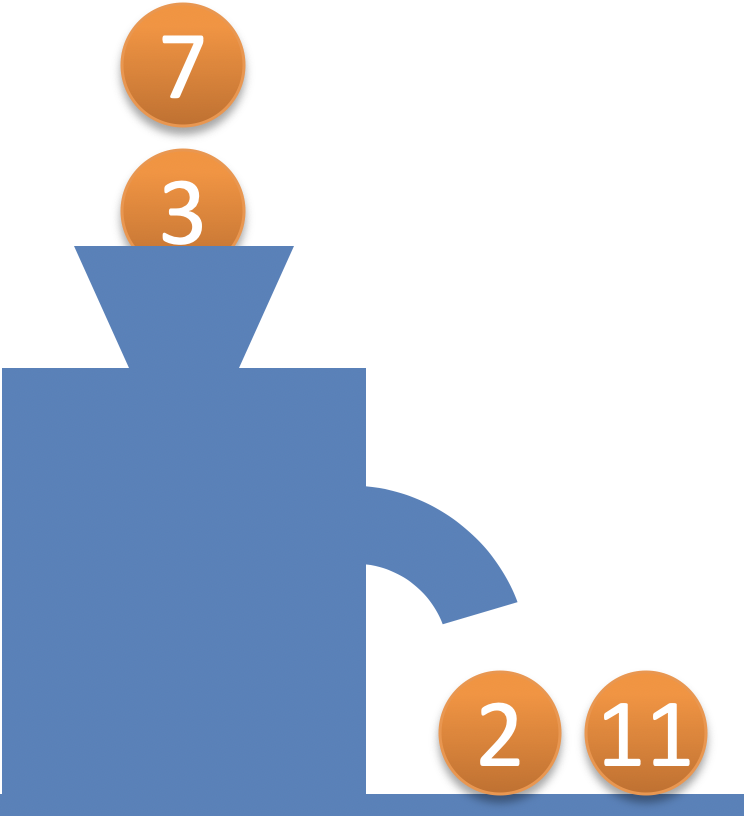
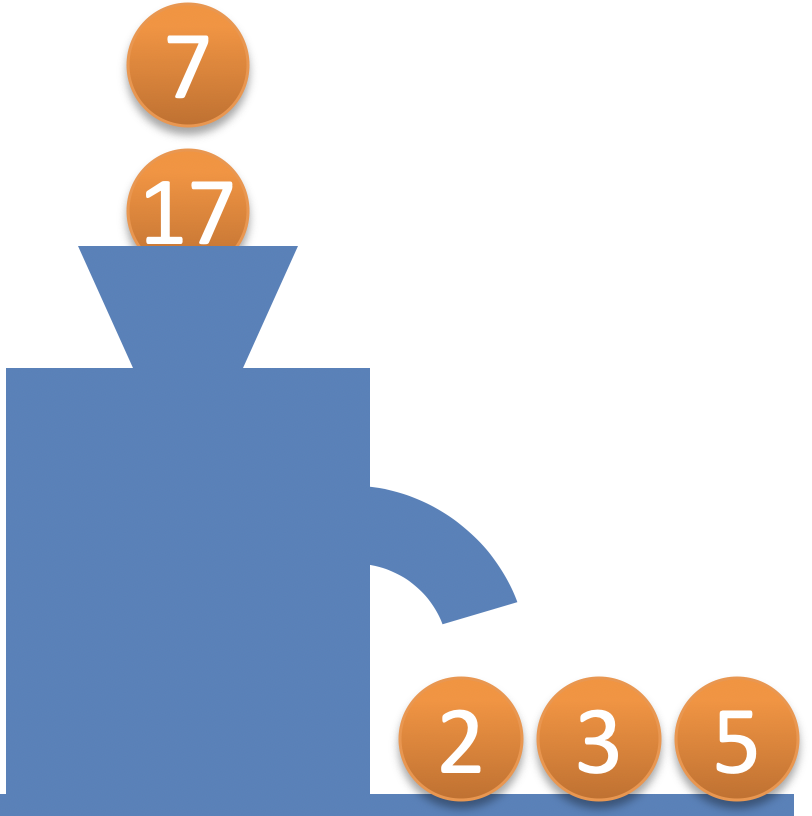
Offenbar werden Primzahlen in den Trichter geworfen. Und Primzahlen kommen auch wieder heraus.
Welchen Zusammenhang gibt es zwischen Ein- und Ausgabe?
Im ersten Beispiel werden die Prinzahlen 2, 3 und 5 eingeworfen. Deren Produkt ist 30. Ausgegeben wird 31
Im zweiten Beispiel werden die Prinzahlen 3 und 7 eingeworfen. Deren Produkt ist 21. Ausgegeben werden 2 und 11 (Produkt: 22).
In beiden Fällen gilt also: Das Produkt der Eingabezahlen wird um eins erhöht. Ausgegeben werden die Primfaktoren dieser Zahl.
Das dritte Beispiel klärt ein (hier unwichtiges) Detail: 7⋅17+1 = 120 = 2^3⋅3⋅5. Jeder Primfaktor wird nur einmal ausgegeben.
Euklid hat mit diesem Automaten (in immaterieller Form) bewiesen, dass es unendlich viele Primzahlen gibt. Dazu hat er zunächst festgestellt, dass unten immer andere Primzahlen herauskommen, als oben eingeworfen werden. Das um eins erhöhte Primzahlprodukt lässt sich ja durch keine dieser Primzahlen teilen, denn immer bleibt der Rest eins. Also ist es selbst eine Primzahl oder das Produkt aus Primzahlen, die nicht eingeworfen wurden.
Angenommen, es gäbe es nur endlich viele Primzahlen. Dann könnte man sie alle in den Automaten werfen, und heraus käme mindestens eine weitere Primzahl. Die Annahme war also falsch.
Bitte machen Sie sich klar, dass Euklids Automat auch funktioniert, wenn das Produkt der eingeworfenen Primzahlen um 1 verkleinert wird. Was käme dann bei den drei Beispielen heraus?
Ein echter altgriechischer Automat
Wenn Sie meinen, die alten Griechen hätten nur philosophiert und mit Technik nichts am Hut gehabt, dann schauen Sie sich doch mal den Mechanismus von Antikythera an!
Fortsetzung: Primzahl-Spielwiese