Kreuzungsfreie Graphen

In der Praxis ist es oft wichtig, einen Graphen so in der Ebene anzuordnen, dass sich keine Kanten kreuzen. Ein typisches Beispiel: Leiterbahnen auf einer Platine.

Betrachten Sie bitte den „vollständigen Graphen“ K₄, bei dem jeder der vier Knoten mit jedem anderen verbunden ist:

Hier kreuzen sich zwei Kanten. Aber das lässt sich ändern: Schieben Sie mit der Maus oder dem Finger den Knoten 3 nach oben (in das Dreieck 4,1,2). Der Graph K₄ kann also ohne Kreuzungen dargestellt werden.

Nun betrachten Sie bitte den „vollständigen bipartiten Graphen“ K_3,2, bei dem die Knoten aus zwei Gruppen (mit 3 und 2 Mitgliedern) bestehen, so dass jeder Knoten genau mit jedem Knoten der anderen Gruppe verbunden ist:

Sicher gelingt es Ihnen auch hier, die Knoten so zu verschieben, dass keine Kreuzung mehr übrig bleibt: Der K_3,2 ist also ebenfalls ein planarer Graph!

Jetzt kommt eine schwierigere Aufgabe. Versuchen Sie sich an dem Graphen K₅:

Gelingt es Ihnen, die Knoten so zu verschieben, dass statt der anfänglich 5 Kreuzungen nur eine übrig bleibt? Dann herzlichen Glückwunsch! Besser geht es nicht. Der K₅ ist nämlich nicht planar!
Bisher haben wir den Nachweis der Planarität durch erfolgreiches Probieren bewiesen. Misserfolg nach langem Probieren ist natürlich kein Beweis, dass es nicht doch geht. Jetzt müssen wir wirklich mathematisch an das Problem herangehen.

Zwei Beispiele für nicht planare Graphen

K₅ ist nicht planar!

Wir nehmen einmal an, der K₅ wäre planar.
Dann würde eine kreuzungsfreie Darstellung die Ebene in Gebiete zerlegen, für deren Anzahl g nach dem Euler’schen Polyedersatz g = k - e + 2 gilt, wobei k die Anzahl der Kanten und n die Anzahl der Knoten (Ecken) ist.
In unserem Fall ist also g = 10 - 5 + 2 = 7 a sei die durchschnittliche Anzahl der Kanten um ein Gebiet.
Jedes Gebiet wird von mindestens 3 Kanten umrandet. Also ist \pink{a \ge 3}

Da jede Kante an zwei Gebiete grenzt, gilt

\pink{a} = \frac{2 k}g = \frac{20}7 \pink{< 3}

Die beiden Ungleichungen widersprechen sich. Demnach war unsere Annahme (K₅ wäre planar) falsch.

K_3,3 ist nicht planar!

Auch an diesem Graphen werden Sie verzweifeln, wenn Sie versuchen, ihn kreuzungsfrei zu machen:

Der K_3,3 wird auch als „Versorgungsgraph“ bezeichnet.

Man kann nämlich die eine Dreiergruppe als Häuser ansehen und die andere z.B. als Wasserwerk, E-Werk und Gaswerk und versuchen, alle Zuleitungen kreuzungsfrei zu verlegen.

Der Beweis, dass der K_3,3 nicht planar ist, klappt ebenso wie beim K₅. Einziger Unterschied: Da die Kanten immer zwischen zwei Gruppen wechseln, muss jedes Gebiet von einer geraden Zahl von Kanten umgeben sein und daher von mindestens vier Kanten!

Der Satz von Kuratowski

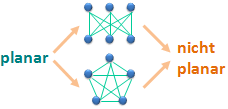
Wir haben gerade zwei Beispiele für nicht planare Graphen gefunden. Der polnische Mathematiker Kazimierz Kuratowski veröffentlichte 1930 einen erstaunlichen Satz. Danach haben unsere beiden Beispiele eine ganz besondere Bedeutung: Mindestens eines dieser beiden Beispiele steckt nämlich in in jedem nicht planaren Graphen!

Eine Unterteilung entsteht, wenn man auf einer Kante einen neuen Knoten einfügt (und damit die Kante in zwei Kanten zerlegt). Wir schauen uns das an einem Beispiel an:

Beispiel: Der Petersen-Graph

Obwohl dieser „Petersen-Graph“ dem K₅ sehr ähnlich sieht (ignorieren Sie bitte zunächst die grauen Knoten!), steckt im Sinne von Kuratowski der K₅ nicht darin!

Bitte schieben Sie nun alle Knoten des Petersen-Graphen (1 bis 10) möglichst genau über die grauen Pendants mit den negativen Nummern.

Das Ergebnis sieht dem K_3,3 ähnlich! Ohne die Kanten zwischen den Knoten 3 und 8 sowie zwischen den Knoten 7 und 9 bleibt eine Unterteilung des Graphen K_3,3 (die vier Kanten {2,4}, {2,10}, {4,6} und {6,10} sind unterteilt).

Nach dem Satz von Kuratowski ist der Petersen-Graph also nicht planar.