
2. Summen von Quadrat- und Kubikzahlen
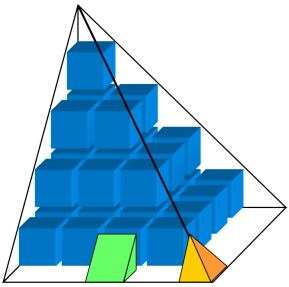
In der Abbildung sehen Sie die Summe der Quadratzahlen
1^2+2^2+3^2+4^2 aus Einheitswürfeln.
Mit Halbwürfeln und
Mini-Pyramiden können wir die
Stufenpyramide zu einer glatten Pyramide mit der Grundfläche (n+1)\cdot(n+1)
und der Höhe n+1 ergänzen.
Diese
Pyramide hat also das Volumen (n+1)^3/3.
Dazu brauchen wir am Rand der Ebene i (von oben gezählt)
2\cdot i Halbwürfel,
außerdem je eine Mini-Pyramide
(Volumen 1/3) in jeder Etage und noch eine ganz oben.
Damit ergibt sich:
\frac{(n+1)^3} 3 = \blue{\displaystyle{\sum_{i=1}^n {i^2}}}
+ \green{\displaystyle{\sum_{i=1}^n i}}
+ \ocher{\displaystyle{\frac{(n+1)} 3}}
Wir lösen die Gleichung nach der gesuchten (blauen) Summe auf und setzen für die grüne Summe die schon bekannte Formel ein:
\begin{aligned}
\blue{\displaystyle{\sum_{i=1}^n {i^2}}} & = \frac{(n+1)^3} 3
- \green{\displaystyle{\frac{n(n+1)} 2}} - \ocher{\displaystyle{\frac{(n+1)} 3}} \cr
& = \gray{\displaystyle{\frac{(n+1)} 6}} (2(n+1)^2 - \green{3n} -\ocher2)) \cr
& = \frac{(n+1) (2n^2 + n)} 6 \cr
& = \blue{\displaystyle{\frac{n(n+1)(2n+1)} 6}}
\end{aligned}

Summen von Kubikzahlen
Mit dem nebenstehend abgebildeten Trick kann man sogar Summen von Kubikzahlen geometrisch darstellen:
Die blauen Rahmen umfassen (von links unten nach rechts oben)- ein einzelnes Quadrat (Fläche:
1^3), - 3 Quadrate mit der Kantenlänge 3 (Gesamtfläche:
3^3), - 5 Quadrate mit der Kantenlänge 5 (Gesamtfläche:
5^3).
Das kann man so für alle ungeraden Zahlen fortsetzen.
In die Zwischenräume packen wir
die geraden Kubikzahlen 2^3 und 4^3 in Form von
2 Quadraten mit der Kantenlänge 2 und 4 Quadraten mit der Kantenlänge 4.
Die Quadrate passen zwar nicht genau, aber die frei bleibenden Flächen werden
exakt durch die doppelt belegten Flächen ausgeglichen.
Offenbar ist also 1^3+2^3+3^3+4^3+5^3 = (1 + 2 + 3 + 4 + 5)^2.
Allgemein gilt demnach die erstaunliche Formel:
\sum_{i=1}^n{i^3} = {\left( \sum_{i=1}^n i \right) }^2
Mit der schon bekannten Formel
\sum_{i=1}^n i = \frac{n(n+1)} 2
ergibt sich daraus
\sum_{i=1}^n{i^3}
= {\left(\frac{n(n+1)} 2 \right)}^2
= \frac{n^2(n+1)^2} 4
Fortsetzung: Summen höherer Potenzen