
Die folgenden Beispiele verwenden die von Gauß und Legendre unabhängig entdeckte Methode der kleinsten Quadrate, um eine Linearkombination (eine Summe von Vielfachen) gegebener Funktionen zu bestimmen, die sich einer Zielfunktion möglichst gut annähert.
Das Problem
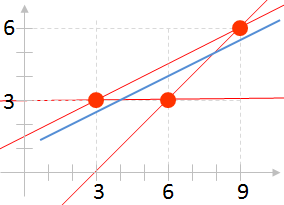
Angenommen, wir beobachten ein Objekt, das sich auf einer Geraden durch die Ebene bewegt. Drei aufeinanderfolgende Messungen liefern die Bahnpunkte (3,3), (6,3) und (9,6).
Wie die Abbildung zeigt, gibt es keine Gerade durch diese drei Messpunkte. Man könnte nun einfach einen Messwert ignorieren und bekäme je nach Wahl eine der drei roten Geraden. Bei einem fehlerbehafteten Messgerät werden aber alle Messungen ähnliche Abweichungen haben, so dass eine vermittelnde Gerade in der Regel zu einem besseren Ergebnis führt.
In der Abbildung ist die maximale Abweichung der blauen Geraden von den Messpunkten kleiner als bei jeder der drei roten Geraden.
Konkret suchen wir eine Gerade
\green{f(x)} = a\yellow x + b
mit den unbekannten Koeffizienten a und b.
Durch Einsetzen der drei Messwerte erhalten wir:
\begin{aligned}
\yellow 3 a + b & = \green 3 \cr
\yellow 6 a + b & = \green 3 \cr
\yellow 9 a + b & = \green 6
\end{aligned}
Das schreiben wir als Matrizengleichung: A\mathbf{x} = \mathbf{b} mit
A = \begin{pmatrix}3 & 1 \cr
6 & 1 \cr
9 & 1 \end{pmatrix}
\quad
\textbf x = \begin{pmatrix}a \cr b \end{pmatrix}
\quad
\textbf b = \begin{pmatrix}3 \cr 3 \cr 6\end{pmatrix}
Dieses Gleichungssystem ist überbestimmt und nicht lösbar.
Die Lösung
In der Vorlesung Lineare Algebra für Informatiker wird der folgende Satz gezeigt:
Satz
Das Normalsystem A^\mathrm{T}A\mathbf{x} = A^\mathrm{T}\mathbf{b} eines linearen Gleichungssystems A\mathbf{x} = \mathbf{b} ist konsistent.
Seine Lösungen sind die Näherungslösungen von A\mathbf{x} = \mathbf{b} mit \mathrm{proj}_W(\mathbf{b}) = A\mathbf{x}
wobei W der Spaltenraum von A ist.
Wir wenden den Satz auf unser Beispiel an.
Für A^\mathrm{T} schreibt man in mathGUIde A.transpose()
Damit erhalten wir die Gerade f(x) = 0.5x + 1
Wir plotten diese Funktion und zeigen dazu die Messpunkte an:
Mehr Komfort: Die Funktion fit
Um uns den Matrixansatz zu ersparen, bietet mathGUIde die Funktion fit an, die aus den Messwerten und dem Funktionstyp direkt die Koeffizienten für die gesuchte Funktion berechnet.
Die Funktion fit erwartet zwei Parameter
- Eine Liste mit den Datenpunkten, jeweils (x,y)
- Eine Liste mit Elementarfunktionen, aus denen die Näherungsfunktion für die Punkte als Linearkombination zusammengesetzt wird
Für unser Beispiel:
Weitere Beispiele
Beispiel 1
Gesucht ist eine Gerade der Form f(x) = ax+b, die die drei
Punkte (3,3), (6,4) und (9,6) möglichst gut approximiert (Regressionsgerade).
mathGUIde hat (hier in etwas vereinfachter Form) die Funktion
f(x) = x/2 + 4/3 geliefert.
Zur Kontrolle der Approximation schauen wir uns einen Funktionsplot an. Dabei ersparen wir uns diesmal das manuelle Zusammensetzen der Funktionen.
Die Funktion fitFn ruft fit auf und gibt dann die zusammengesetzte Funktion aus:
Beispiel 2
Eine Parabel soll an vier Punkte angenähert werden:
Kontrolle des Ergebnisses:
Beispiel 3
Transzendente Funktion: f(x) = a + b \, x \log x + c \, e^x
Gesucht sind die Koeffizienten a, b, c
Kontrolle des Ergebnisses:
