Netzwerke aus elektrischen Widerständen

Die Aufgabenstellung

Zwischen zwei Punkten eines Netzwerks aus elektrischen Widerständen wird eine Spannung U angelegt. Gesucht ist der Strom I, der nun durch das Netzwerk fließt.

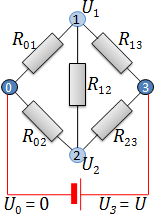
Im nebenstehenden Bild sind die Anschlusspunkte dunkelblau, die übrigen Knotenpunkte des Netzwerks hellblau markiert. Wir nummerieren die Knoten ab Null durch, wobei wir 0 und die höchste Zahl (im Bild 3) für die Anschlusspunkte verwenden. Den Widerstand zwischen den Knoten i und k bezeichnen wir mit R_{ik} und den Strom, der vom Knoten i zum Knoten k fließt, mit I_{ik}. Da der Strom eine Richtung hat, ist I_{ki} = -I_{ik}.

Das Ohm’sche Gesetz

Nach dem Ohm’schen Gesetz ist die Spannung zwischen zwei durch einen Widerstand verbundenen Knoten gleich dem Produkt aus Widerstand und durchfließenden Strom:

U_i - U_k = R_{ik} I_{ik}

Mit dem Leitwert (Kehrwert des Widerstandes) ergibt sich daraus

I_{ik} = \sigma_{ik} (U_i - U_k)

Wir schreiben das für die Leitwerte der fünf Widerstände hin:

\begin{aligned} \yellow{I_{01}} & = & \sigma_{01} U_1 \cr \yellow{I_{02}} & = & \sigma_{02} U_2 \cr \yellow{I_{12}} & = & \sigma_{12} (U_2 - U_1) \cr \yellow{I_{13}} & = & \sigma_{13} (U - U_1) \cr \yellow{I_{23}} & = & \sigma_{23} (U - U_2) \end{aligned}

Die erste Kirchhoff’sche Regel

Nun betrachten wir die erste Kirchhoff’sche Regel. Diese sagt einfach, dass kein Strom verloren geht: Die Summe der in einen Knotenpunkt hineinfließenden Ströme ist gleich der Summe der herausfließenden Ströme. (Oder noch einfacher, wenn man hineinfließenden Ströme als negative herausfließenden Ströme ansieht: Die Summe der von einem Knoten wegfließenden Ströme ist Null.)

Wir wenden die erste Kirchhoff’sche Regel für alle inneren Knoten (im Beispiel 1 und 2) an:

\begin{aligned} I_{01} & = I_{12} + I_{13} \cr I_{02} & = I_{21} + I_{23} \cr \end{aligned}

Da allgemein I_{ik} = -I_{ki} ist, verwenden wir besser nur Ströme von einem kleinerem zu einem größeren Index:

\begin{aligned} \yellow{I_{01}} & = \yellow{I_{12}} + \yellow{I_{13}} \cr \yellow{I_{02}} & = -\yellow{I_{12}} + \yellow{I_{23}} \end{aligned}

Kombination der Gleichungen

Nun setzen wir die durch das Ohm’sche Gesetz gewonnenen Gleichungen in die mit der Kirchhoff’schen Regel gewonnenen Gleichungen ein:

\begin{aligned} \sigma_{01} U_1 & = \sigma_{12} (U_2 - U_1) + \sigma_{13} (U - U_1) \cr \sigma_{02} U_1 & = -\sigma_{12} (U_2 - U_1) + \sigma_{23} (U - U_2) \end{aligned}

Nach den Unbekannten U_1 und U_2 gegliedert, ergibt sich:

\begin{aligned} (\sigma_{01} + \sigma_{12} + \sigma_{13}) U_1 - \sigma_{12} U_2 & = \sigma_{13} U \cr -\sigma_{12} U_1 + (\sigma_{02} + \sigma_{12} + \sigma_{23}) U_2 & = -\sigma_{23} U \end{aligned}

Wir müssen also das Gleichungssystem

\begin{pmatrix} \sigma_{01} + \sigma_{12} + \sigma_{13} & - \sigma_{12} \cr -\sigma_{12} & \sigma_{02} + \sigma_{12} + \sigma_{23} \end{pmatrix} \cdot \begin{pmatrix}U_1 \cr U_2\end{pmatrix} = \begin{pmatrix}\sigma_{13} U \cr \sigma_{23} U\end{pmatrix}

lösen.

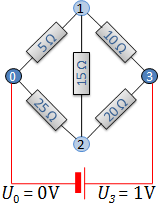
Dazu betrachten wir konkrete Widerstände, setzen U_3 auf 1V und lassen die Dimensionen weg:

\begin{pmatrix} \frac 1 5 + \frac 1 {15} + \frac 1 {10} & - \frac 1 {15} \cr -\frac 1 {15} & \frac 1 {25} + \frac 1 {15} + \frac 1 {20}\end{pmatrix} \cdot \begin{pmatrix}U_1 \cr U_2\end{pmatrix} = \begin{pmatrix}\frac 1 {10} \cr \frac 1 {20}\end{pmatrix}

Dieses Gleichungssystem kann mathGUIde für uns lösen:

Der Gesamtwiderstand

Wir kennen jetzt die Spannung zwischen den inneren Knoten (1, 2) und dem Ausgangsknoten (0). Der Rest ist einfach: Mit dem Ohm’schen Gesetz berechnen wir die beiden vom Ausgangsknoten wegfließenden Ströme:

\begin{aligned} I_{01} & = \frac {U_1} {R_{01}} = U_1 \sigma_{01} \cr I_{02} & = \frac {U_1} {R_{02}} = U_2 \sigma_{02} \end{aligned}

Mit der ersten Kirchhoff’schen Regel berechnen wir nun den Gesamtstrom durch das Netzwerk. Der verteilt sich am Eingangsknoten (0) auf die beiden Zweige nach Knoten 1 und 2:

I = I_{01} + I_{02}

Damit ergibt sich der Gesamtwiderstand:

R = \frac U I = \frac {1V} I

Zusammenfassung des Verfahrens

1. Die Knoten des Netzwerks von Null bis n durchnummerieren, wobei die Indizes 0 und n für die Anschlussknoten verwendet werden.
2. Für jede Kante (Widerstand) das Ohm’sche Gesetz in der Form I = σU hinschreiben.
3. Für jeden inneren Knoten (1 bis n-1) die 1. Kirchhoff’sche Regel hinschreiben.
4. In den in Schritt 3 hingeschriebenen Regeln die Ströme durch die rechten Seiten der Gleichungen aus Schritt 2 ersetzen.
5. Die Gleichungen aus Schritt 4 nach den Unbekannten U_1 bis U_{n-1} gliedern und U_0 auf Null (Volt) und U_n auf 1 (Volt) setzen.
6. Das Gleichungssystem lösen.
7. Mit Hilfe der nun bekannten Knotenspannungen und des Ohm’schen Gesetzes die Summe I der vom Knoten Null ausgehenden Ströme berechnen.
   Daraus dann wiederum mit dem Ohm’schen Gesetz den Gesamtwiderstand 1/I (Ω) berechnen.

Übungsaufgabe

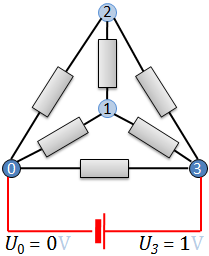
Sechs Widerstände von 10 Ω, 12 Ω, 15 Ω, 18 Ω, 22 Ω und 27 Ω werden zu einem Tetraeder verlötet.

Schreiben Sie ein mathGUIde-Programm, das folgendes ausgibt:

1. Die Anzahl unterschiedlicher möglicher Widerstände zwischen zwei Ecken eines solchen Tetraeders,
2. den niedrigsten und den höchsten dieser Widerstände,
3. den größten prozentualen Sprung zwischen zwei aufeinanderfolgenden sortierten Widerständen.

Hinweise

• Verwenden Sie die mathGUIde-Funktion permutations, um alle möglichen Anordnungen der Widerstände zu ermitteln.
• Bauen Sie einen Array aller möglichen Widerstände auf.
• Sortieren Sie mit der Array-Methode sort).
• Das folgende kleine Beispiel zeigt Ihnen technische Mittel, die Sie zur Lösung verwenden können:
  Gesucht sind alle Zahlen (in aufsteigender Reihenfolge), die sich in der Form \frac a b + \frac c d schreiben lassen, wobei a, b, c und d die Zahlen 1, 2, 3 und 4 in beliebiger Reihenfolge sind.
   
a = permutations([1,2,3,4]) .map(p => p[0]/p[1] + p[2]/p[3]).sort() s = new Set(a) // Duplikate entfernen :s

Wegen der Kommutativität der Addition (a/b + c/d = c/d + a/b) ist klar, dass jede Zahl mindestens zweimal in den Array l aufgenommen wird.